Obiettivi

Questo tutorial ha lo scopo di introdurre solo il pacchetto pomodoro, utilizzando un case study. Lo scopo di questo pacchetto è modellare e riportare facilmente la modellazione predittiva.

Dataset

Dopo aver pulito il set di dati per questo caso di studio, possiamo visualizzare le statistiche riassuntive dei dati forniti.

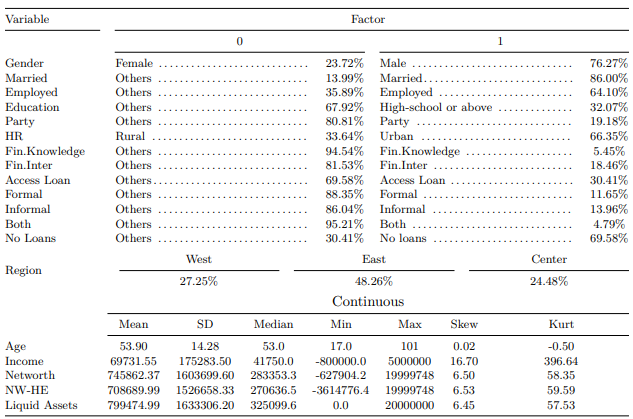
Summary Statistics
Summary Statistics

Nota: HR sta per Household Registration. NW-HE è il patrimonio netto meno il patrimonio immobiliare. Tutte le variabili dell’asset (ad es. reddito, patrimonio netto, NW-HE e attività liquide sono in renminbi cinese (CNY).

Overview

Il pacchetto pomodoro esegue attualmente bagging (BAG_Model), boosting (GBM_Model), random forest (RF_Model), modelli logistici multinominali (MLM_Model) e logistici (GLM_Model). Questo pacchetto è utile quando è necessario confrontare la modellazione predittiva utilizzando le diverse suddivisioni dei dati o/e l’aggiunta di variabili esogene nell’equazione. E divide il set di dati in set di treno/test 80/20, utilizzando un campionamento casuale stratificato e implementa 10 convalide incrociate per ciascun modello.

Installation

Puoi installare pomodoro da CRAN con:

install.packages("pomodoro")
library(pomodoro)

Building a Selected Model

Costruiamo RF_Model uno dei modelli disponibili per questo pacchetto. Nel pomodoro campo aiuto possiamo vedere che RF_Model è stato definito come RF_Model(Data, xvar, yvar).

DataSet

Per scopi computazionali prendiamo le prime 1000 righe di sample_data.

sample_data <- sample_data[c(1:1000),]

Selecting Dependent Variables

dove xvar è un vettore definito come di seguito:

xvar <- c("sex", "married", "age", "havejob", "educ", "political.afl",
 "rural", "region", "fin.intermdiaries", "fin.knowldge", "income")

Selecting Independent Variables

dove “yvar” è una variabile fattore a due o più livelli definita come di seguito:

yvar <- c("Loan.Type")

o

yvar <- c("multi.level")

Implemantation

Possiamo implementare RF_Model per yvar <- c("multi.level") come segue,

 yvar <- c("multi.level")
 xvar <- c("sex", "married", "age", "havejob", "educ", "political.afl",
 "rural", "region", "fin.intermdiaries", "fin.knowldge", "income")
 set.seed(123) # set.seed() for the reproducible outcome.
 BchMk.RF <- RF_Model(sample_data, xvar, yvar)

Results of the RF_Model

Usando attributes(BchMk.RF), possiamo vedere le opzioni di risultato.

BchMk.RF$results

  mtry  Accuracy     Kappa AccuracySD    KappaSD
1    2 0.7640207 0.1712487 0.01929120 0.06294866
2    6 0.7288629 0.1729132 0.06145650 0.15118984
3   11 0.7264250 0.1782029 0.03964603 0.11603731

head(BchMk.RF$Pred_prob)

    zero   one
1  0.912 0.088
3  0.968 0.032
4  0.520 0.480
12 0.898 0.102
24 0.922 0.078
33 0.956 0.044

BchMk.RF$Roc

Call:
multiclass.roc.default(response = Y.test, predictor = Pred.prob)

Data: multivariate predictor Pred.prob with 2 levels of Y.test: zero, one.
Multi-class area under the curve: 0.7143

BchMk.RF$ConfMat

      Y.test
       zero one
  zero  140  43
  one     8   8

BchMk.RF$ACC

[1] 0.7437186

Building an Estimated Models

Per modellare tutto il set di dati e le sue suddivisioni, in modo intercambiabile con 3 asset che possiedono variabili (networth, networth_homequity e liquid.assets) e data una variabile esogena, in questo caso exog = "political.afl".

Costruiamo di nuovo RF_Model ma questa volta . Nel pomodoro campo aiuto possiamo vedere che Estimate_Models è stato definito come Estimate_Models(DataSet = Data, yvar, exog = NULL, xvec = xvar, xadd, type, dnames).

Abbiamo già definito xvar, yvar e Data.

Selecting exog Variable

exog = "political.afl" definirà il set di dati in base ai livelli dei fattori di "political.afl" in questo caso “0” e “1”.

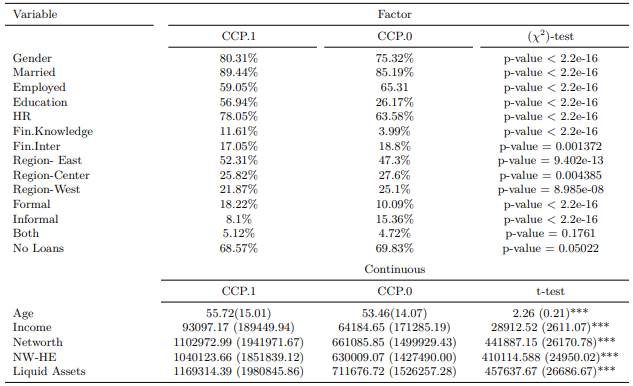
Summary Statistics
Summary Statistics

Nota: HR sta per Household Registration. NW-HE è il patrimonio netto meno il patrimonio immobiliare. Tutte le variabili dell’asset (ad es. reddito, patrimonio netto, NW-HE e attività liquide sono in renminbi cinese (CNY).

Selecting xadd Variable

xadd è un insieme di vettori che non sono altamente correlati con "reddito" ma altamente correlati tra loro. Quindi dobbiamo aggiungere ogni variabile in xadd = c("networth", "networth_homequity", "liquid.assets") in modo intercambiabile.

Selecting type Variable

type può essere uno dei modelli di bagging (BAG), boosting (GBM), random forest (RF), multinominal logistic (MLM), and logistic models (GLM).

Selecting dnames Variable

dnames è il valore dei fattori di exog. Ad esempio dnames = c("0","1") poiché ci sono 2 livelli in exog = "political.afl" che è “0” e “1”. L’argomento dnames è importante per evitare confusione quando si stampano i risultati.

Implemantation

Possiamo implementare Estimate_Models per yvar <- c("multi.level") come segue,

CCP.RF <- Estimate_Models(sample_data, yvar, xvec = xvar, exog = "political.afl",
 xadd = c("networth", "networth_homequity", "liquid.assets") ,
 type = "RF", dnames = c("0","1"))

Results of the Estimate_Models

Usando CCP.RF, possiamo vedere i risultati di BchMk+networth, BchMk+networth_homequity, BchMk+liquid.assets D.0+patrimonio netto, D.0+equità_patrimoniale_patrimoniale, D.0+asset.liquidi, “D.1+patrimonio netto”, “D.1+patrimonio_patrimoniale_patrimoniale” e “D.1+attivo.liquido”.

Estimate_Models ha implementato RF_Model, in primo luogo per tutti i set di dati come viene chiamato BchMk, in secondo luogo D.0 e infine D.1, aggiungendo 3 variabili di asset in modo intercambiabile.

Dove D.0 e D.1 derivano da dnames = c("0","1") e può essere interpretato come D.0 quando political.afl == 0 e D.1 quando political.afl == 1

Estimate_Models ha riportato BchMk con tutte le variabili exog e diviso tutto il set di dati (BchMk) a 2 livelli, quando l’osservazione ha political.afl == 0 o political.afl == 1,

Poiché si tratta di un oggetto elenco, dobbiamo utilizzare attributi come segue,

attributes(CCP.RF$EstMdl$`D.1+liquid.assets`)
> CCP.RF$EstMdl$`D.1+liquid.assets`$results
  mtry  Accuracy     Kappa AccuracySD   KappaSD
1    2 0.7926901 0.3348631 0.04543311 0.1835925
2    6 0.7929825 0.3707344 0.03656725 0.1258099
3   11 0.7979532 0.3894589 0.03274767 0.1245565
> head(CCP.RF$EstMdl$`D.1+liquid.assets`$Pred_prob)
    zero   one
3  0.992 0.008
4  0.124 0.876
8  0.290 0.710
25 0.742 0.258
33 0.854 0.146
36 0.750 0.250
> CCP.RF$EstMdl$`D.1+liquid.assets`$Roc

Call:
multiclass.roc.default(response = Y.test, predictor = Pred.prob)

Data: multivariate predictor Pred.prob with 2 levels of Y.test: zero, one.
Multi-class area under the curve: 0.8182
> CCP.RF$EstMdl$`D.1+liquid.assets`$ConfMat
      Y.test
       zero one
  zero   29   4
  one     5   7
> CCP.RF$EstMdl$`D.1+liquid.assets`$ACC
[1] 0.8

Building a Combined Performance

Estimate_Models ha riportato risultati predittivi sia per political.afl == 0 che per political.afl == 1. Ciò di cui abbiamo bisogno è combinare questi set di dati divisi per calcolare su tutte le prestazioni per il divisione dei dati sull’affiliazione politica.

Nel pomodoro campo aiuto possiamo vedere che Combined_Performance è stato definito come Combined_Performance(Sub.Est.Mdls).

Abbiamo già definito tutto ciò di cui abbiamo bisogno in Estimate_Models, riuniamoli.

Implemantation

Sub.CCP.RF <- list(Mdl.1 = CCP.RF$EstMdl$`D.1+networth`,
Mdl.0 = CCP.RF$EstMdl$`D.0+networth`)
CCP.NoCCP.RF <- Combined_Performance(Sub.CCP.RF)

Results of the Combined_Performance

Usando attributes(CCP.NoCCP.RF) possiamo vedere i risultati di Combined_Performance

head(CCP.NoCCP.RF$Pred_prob)

    zero   one
58 0.120 0.880
60 0.822 0.178
61 0.116 0.884
75 0.980 0.020
80 0.402 0.598
85 0.950 0.050

CCP.NoCCP.RF$Roc

Call:
multiclass.roc.default(response = Combine.Mdl$Actual, predictor = Pred_prob)

Data: multivariate predictor Pred_prob with 2 levels of Combine.Mdl$Actual: zero, one.
Multi-class area under the curve: 0.6929

CCP.NoCCP.RF$ConfMat

      one zero
  one   11    4
  zero  39  143

CCP.NoCCP.RF$ACC

> CCP.RF$EstMdl$`D.1+liquid.assets`$ACC
[1] 0.7817259

Divertiti!

Back to top